快速排序

你也许会被快速排序的文章弄得迷迷糊糊，其实大体上去看，快速排序就一步：找个数做基准数，把小于它的数移到它左边，把大于它的数移到它右边。这句话是核心。然后我们只需要让基准数左边的重复上面的步骤，让基准数右边的再重复上面的步骤就完了。

比如我们有一个数组：

int[] nums = {5, 2, 6, 8, 4, 7, 9, 1};

快速排序的思想就是使用递归，其实使用递归并不是多么复杂，在理解算法的思想后，只需要关注算法中重复的步骤，那就是递归的核心代码。

比如快速排序的算法思想，大体代码如下：

public void quick(int left, int right) {    /*    * 给这段代码起个名字为：基准校验    * 把小于基准数的移到左边，把大于基准数的移到右边    */    quick(left, now); //继续处理左边的    quick(now, right); //继续处理右边的}

经过一遍基准校验，我们就找到了该基准数在完全排序后的正确位置！

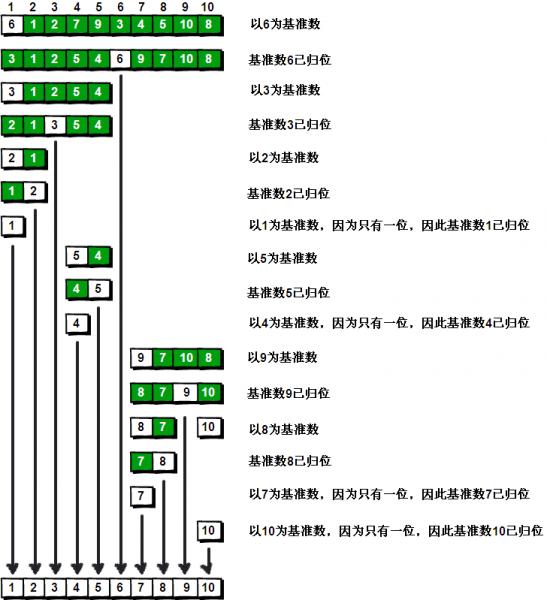
写出上面的大体算法步骤，就表示我们已经有了雏形，现在该如何实现找个数做基准数，把小于它的数移到它左边，把大于它的数移到它右边呢？

排除不满足的情况：

//已经不满足条件就代表可以不用递归了        if (left > right) {            return;        }

我们可以定义两个指针，用于遍历数组：

int start = left;//起点下标        int end = right;//终点下标

再找一个基准数：

int temp = nums[left];//把第一个数作为基准点

遍历代码：

/*如果左右指针还没有走到一起，代表还有位置没有遍历*/ while (start != end) {         //右指针先走，找到小于基准数的停止     while (start < end && nums[end] >= temp) {          end--;     //这是往左移动指针     }     //左指针后走，找到大于基准数的停止     while (start < end && nums[start] <= temp) {          start++;  //这是往右移动指针     }     //如果左右指针在未相遇时都找到了目标，则交换位置     if (start < end) {             int i = nums[start];         nums[start] = nums[end];         nums[end] = i;     }     //左右指针走到一起，则遍历结束 } //把基准数与该点交换位置，因为这就是基准数的正确位置 nums[left] = nums[start]; nums[start] = temp;

如果还是不太清楚，不如自己动手试试！

拷贝完整代码：

//定义一个数组    static int[] nums = {
   5, 2, 6, 8, 4, 7, 9, 1};    static int n = nums.length - 1;    /**     * 递归的数据结构就是栈     * left right代表该段数组的起点和终点     */    public void quick(int left, int right) {        //已经不满足条件就可以不用递归了        if (left > right) {            return;        }        //定义俩指针 用于移动        int start = left;//起点下标        int end = right;//终点下标        int temp = nums[left];//把第一个数作为基准点        pri(left, right);//打印此时的结果，不用在意        while (start != end) {    //如果左右指针还没有走到一起，代表还有位置没有遍历            while (start < end && nums[end] >= temp) { //右指针先走，找到小于基准数的停止                end--;            //这是往左在移动指针            }            while (start < end && nums[start] <= temp) { //左指针后走，找到大于基准数的停止                start++;     //这是往右在移动指针            }            if (start < end) {    //如果左右指针在未相遇时都找到了目标，则交换位置                int i = nums[start];                nums[start] = nums[end];                nums[end] = i;            }        }        //此时的left和right走到了一起        //把基准数与该点交换位置        nums[left] = nums[start];        nums[start] = temp;        prin(start);//打印输出，不用在意        //以上代码的作用就是把小于基准数的移到左边，把大于基准数的移到右边        quick(left, start - 1); //继续处理左边的，这里是一个递归的过程        quick(start + 1, right); //继续处理右边的 ，这里是一个递归的过程    }    /**    * 主程序入口    */    public static void main(String[] args) {        new Test().quick(0, n);    }    /**     * 以下代码忽略即可，用于打印输出     */    private void pri(int start, int end) {        StringBuffer s = new StringBuffer();        s.append("对数组 [");        while (start <= end) {            s.append(nums[start] + " ");            start++;        }        s.append("]");        s.append(" 排序");        System.out.print(s);    }    private void prin(int j) {        StringBuffer s = new StringBuffer();        s.append("， 排序后 [");        int start = 0;        while (start <= n) {            if (start == j) {                s.append("(" + nums[start] + ") ");            } else {                s.append(nums[start] + " ");            }            start++;        }        s.append("]");        s.append(" ");        System.out.println(s);    }

打印输出：

对数组 [5 2 6 8 4 7 9 1 ] 排序， 排序后 [4 2 1 (5) 8 7 9 6 ] 对数组 [4 2 1 ] 排序， 排序后 [1 2 (4) 5 8 7 9 6 ] 对数组 [1 2 ] 排序， 排序后 [(1) 2 4 5 8 7 9 6 ] 对数组 [2 ] 排序， 排序后 [1 (2) 4 5 8 7 9 6 ] 对数组 [8 7 9 6 ] 排序， 排序后 [1 2 4 5 6 7 (8) 9 ] 对数组 [6 7 ] 排序， 排序后 [1 2 4 5 (6) 7 8 9 ] 对数组 [7 ] 排序， 排序后 [1 2 4 5 6 (7) 8 9 ] 对数组 [9 ] 排序， 排序后 [1 2 4 5 6 7 8 (9) ]